László SURÁNYI
Descartes,
Bolyai, Lobatschewskij und die Zurückführung der Geometrie zu ihrer subjektiven
Wurzel[1]
1. Während der um das Zentrum gezogene Kreis durch seine Geschlossenheit eine ästhetische, in sich aufnehmende Gebärde darstellt, vergegenwärtigt die Gerade eine aktive ethische Geste, die Hinwendung zum "Du", die Schaffung und die Überwindung des Abstandes, die "vorwärts und aufwärts strebende Rangrelativität" (Lajos Szabó), die Bewegung des Zentrums. Bild und Feuer, Substantiv und Verb, "Wesen und Geist" (Böhme), Formung und Schöpfung.
Doch die Gerade, genauer: das Parallelen-Paar der euklidischen Ebene, stelt auch eine gegensätzliche, Ohmächtigkeit audsrückende Geste dar und setzt sie sogar endlos fort: jene Bewegung, mit der wir das Zentrum, das gleichermaßen Anfangs- und Endpunkt ist, aus dem Raum unserer Anschauung entlassen, so daß seine Bedeutung verblaßt und wir uns nicht mehr mit ihm identifizieren können.
2. Die Richtung ist ein Zeigen, die übereinstimmende Richtung ist ein Zeigen in einen gemeinsamen Punkt,in den gemeinsamen Mittelpunkt. Das gemeinsame Zentrum is kein bloßer mathematischer Punkt, es hat einen Innenraum (wie auch von seiner modernen funktionellen Version, dem Null-Vektor ablesbar): Es enthält mit jeder Richtung Gleiches und zu jeder Richtung Waagegerechtes (das geometrische Zeichen für Dimensionswachstum). Das Origo (Urspungspunkt) ist die Quelle jeder Identifizierung (das Auf-mich-Beziehen der Widerstände) und jeder Transzendierung, des Dimensionswachstums. Die beiden Richtungen, Subjektivierung und Transzendierung, existieren nicht ohneeinander, nur als die beiden einander stärkenden Richtungen des rechten Winkels.
Diesen letzten gemeinsamen Identifikationspunkt, an dem die Gleichgerichteten sich aufeinander beziehen, sich begegnen, schiebt das Bild der euklidischen Parallelen in die Unendlichkeit (und im Falle sich schneidender Geraden reduziert es ihn auf einen bloßen mathematischen Punkt ohne Innenraum).
Der Abstand der euklidischen Parallelen ist hier konstant. Die aus dem Mythos Heraustretenden wenden sich selbst zu und können in gleichem Abstand voneinander auf ihrer Bahn bleiben, ohne Annäherung und Entfernung, ohne Desorientierung, ewige Isolation in der Ebene an.
Parallelen haben weder in ihrer Vergangenheit noch in ihrer Zukunft oder Gegenwart einen gemeinsamen Punkt. Das Gemeinsame ist aus der Vergangenheit in längst vergangenen Zeiten, im entleerten, entthronten Mythos versunken und aus der Zukunft in die unerreichbare Ferne entschwunden. Wir sehen in der Parallelen das Bild einer Gemeinschaft, deren Mitglieder zusammen, aber in unäberbräckbarem Abstand zueinander betrachten, was sich in die verschommenen Mythen längst vergangener und fernab kommender Zeiten zurückgezogen hat. Sie können das gemeinsamen Betrachatete weder als gemeinsame Genesis noch als gemeinsame Erlösung vergegenwärtigen.
Die euklidische Ebene ist die Ebene der Ananke.
3. Auf dieser Ebene, die ihr Zentrum verloren hat, existiert immerhin eine Ähnlichkeit der ebenen Figuren. Das griechische Postivum: auf dem tragischen Hintergrund lebendige Formen schaffen. Auf dem Hintergrund der ewigen Nicht-begegnung die Vergleichbarkeit der lebendigen Formen. Der dynamische Vergleich der abstrakt-archaischen geometrischen Gebilde: ihre Verkleinerung und Vergrößerung.
Maßeinheit des Messens ist das pythagoreische Grundgebilde das Einheitsquadrat. Der positive Inhalt des Parallelenaxioms: Die Identität des Einheitsquadrats ist auf der gesamten Ebene transparent präsent. Die Möglichkeit seiner Verkleinerung und Vergrößerung ist die Grundlage jeder Messung.
4. Mögliche Verkleinerung und Vergrößerung der ebenen Figuren und unveränderbare Ananke, sichtbare pythagoreische Grundformen und unsichtbare Brechung – die (sogenannte hyperbolische) Geometrie von Bolyai/Gauss/Lobatschewskij kehrt all dies um. Sie manifestiert die moderne Tragik in der Sprache der Mathematik.
a/ Bolyai/Gauss/Lobatschewskij entdeckten die asymptotischen Geraden: ihre Parallelen sind asymptotischen Geraden. Ihre Bestimmung wäre es sich zu treffen (ihr Abstand strebt nach 0). Und dennoch treffen sie nicht. (Abb. 3.)
Demgegenüber: Der Origo(=Ursprungspunkt)-Gedanke bedeutet, daß sich auch die scheinbar am stärksten divergierenden Geraden treffen; sie interpretieren sich gegenseitig. Die Begegnung erfolgt in einem Raum von beiderseitigem inneren Interesse. Richtungslose, gleichgültige Geraden, Gedankengänge, die kein Ziel und Gewicht, also keinen bezwungenen inneren Widerstand haben, können sich nicht treffen. Ort der Begegnung ist das Zentrum, der Innenraum des Ursprungspunktes.
b/ Die Geraden von Bolyai/Gauss/Lobatschewskij haben mehr Gewicht, weil sie einen grüßeren Widerstand in sich verdichten und bezwingen wie die von Euklid. Aber noch leben im Dualismus veon Widerstand und Zentrum.
Bolyai/Gauss/Lobatschewskij konstatieren eine Brechung zwischen den parallelen Halbgeraden, dis sie aus dem äußeren Punkt in zwei Richtungen zu derselben Geraden ziehen (Abb. 2.) Damit mahcen wie auf ihre Weise die der Geraden innewohnenden gegensätzlichen, divergierenden Kräfte sichtbar. Die euklidischen Geraden haben nur einen "idealen", "unendlich Fernen" Punkt, ihre Geraden haben zwei, so daß sich bei ihnen Anfangs- und Endpunkt nicht mehr dermaßen vermischen wie bei Euklid, beide haben in der Gegenwart gut Unterscheidbares zu sagen. Aber aus dem Blickwinkel der Geraden besteht keine Kontinuität zwischen den beiden, sondern Brechung, jeder Punkt wird zum Brechungspunkt.
Die Parallelen von Bolyai/Gauss/Lobatschewskij sind das Symbol moderner Tragik: Sie machen die bei Euklid noch unsichtbare Brechung sichtbar. Die unsichtbare Brechung zwischen dem Zeichen und dem Bezeichneten wird auch im Zeichen erkennbar.
5. Die euklidische Eben kehrt sich also bei Bolyai/Gauss/Lobatschewskij um, zeigt ihre Rückseite. In den Vordergrund tritt die Welt des angespannt Tragischen, der ungelösten Widerspruche, der Divergenz (der Bolyai-Raum stehtin enger Verwandtschaft zu den Wirbelräumen von Lajos Vajda[2]) in den Hintergrund gedrängt wird dagegen die Vergleichbarkeit, die formenreiche Welt der Böhmeschen Leiblichkeit, der Rosenzweigschen Lebendigkeit: Auf der hyperbolischen Ebene gibt es keine Ähnlichkeit, läßt sich nichts verkleinern, nichts vergrößern. Es ist schwieriger erreichbar, daß sich zwei Geraden schneiden. Schwieriger entstehen Dreiecke, begrenzte ebene Figuren, weil die Tragik, die sich einander nähernden Parallelen, die Wirbel, die die Begegnung der zur Begegnung bestimmten hemmt, einen wesentlich größeren und akzentuierteren Teil der Ebene einnehmen. Zur Entstehung der Form (Gerade, Dreieck) muß ein größerer Widerstand überwunden werdenm dafür hat die enstehende Form mehr Gewicht. Außerdem ist sie individueller, hat mehr Widerstand gegenüber dem Messen, der Vergleichbarkeit. Das Messen wird wegen der "Krümmung" schwieriger (aber definitiver: es gibt eine absolute Längeneinheit und es gibt ein maximales, jedes Dreieck in sich enthaltendes Dreieck). Die Transparenz der Rechtwinkel-Struktur wird gebrochen: Es gibt kein Quadrat.
(Ein Vergleich mit Béla Bartók liegt auf der Hand. Auch für ihn ist die strenge, sich scheinbar gegen das musikalisch Schöne stemmende Darstellung der hinter den klassischen Gebilden steckenden Brechungen charakteristisch.)
6. Bolyai/Gauss/Lobatschewskij meinen, daß das ausgewogene Verhältnis zwischen den beiden Grundrichtungen -- der Vertikalen des Strebens nach höherem (und letzlich nach maximalem) Wert und der Horizontalen des Strebens nach Sicherung der minimalen Werte --, das Stabilität und Produktivität einer erkennenden Epoche (und ihre Geschichtsperioden überspannende Einheit) gewährleistete, seine Transparenz verloren habe. Sie wollen zur tieferen Bedeutung des Rechtwinkel-Symbols -- zur tieferen Erschließung der aus dem Ursprungspunkt strahlenden Rechtwinkel-Struktur -- vordringen, und das können sie nur erreichen, wenn sie bis zur Wurzel der wider der Transparenz- (und wider dem Rechtwinkel-) wirkenden Widerstände graben und sie in den Mittelpunkt stellen. Dieser Widerspruchsherd ist die Individualität. Die Revolution von Bolyai/Gauss/Lobatschewskij ist die Revolution der Individualität.
7. Diese Revolution wurde ausgelöst von Descartes' (unbewußt) gnostischem Origo(= Ursprungspunkt)-Gedanken, der die euklidische Geometrie arithmetisiert, um sie zu begründen. Doch sein Origo-Gedanke widersetzt sich der bei den euklidischen Parallelen erfolgenden Projektion der Widerstände ins Unendliche sowie dem Auseinanderfallen des Punkt-Innenraumes in der Ebene. Während die euklidische (wie auch die hyperbolische) Auffassung von dem mathematischen Punkt ohne Innenraum und der Geraden als Grundbegriffen ausgeht (der Begriff der auf Intensität verweisenden Richtung ist dem der extensiven Gerade untergeordnet), stellt Descartes das Origo, der Ursprungspunkt, das Zentrum und die aus ihm strahlenden Grundrichtungen – die vertikale und die horizontale Achse – in den Mittelpunkt. Das Origo ist der Anfangspunkt, wo das Cogito als sicherer Ausgangspunkt in die Welt des Sum eindringt und die Struktur des Sum beleuchtet: das heißt die Tatsache, daß das Sum selbst im Schnittpunkt der überzeitlichen Vertikale und der zeitlichen Horizontale steht.
Im Gegensatz zur kopernikanischen Wendung, die die absolute Bedeutung der Grundrichtungen des Mythos – oben und unten, vorne und hinten – ins Wanken bringt beziehungsweise relativiert, erscheint in Descartes' Mathematik der ausgezeichnete Punkt, die ausgezeichnete Richtung und als drittes die ausgezeichnete ebene Figur: der Einheitskreis, das gemeinsame Urbild der Kegelschnitte (Kreis, Ellipse, Parabel, Hyperbel, usw.). Einer der schönsten Gedanken Descartes' ist jenes Origo-Struktur, mit der die Intensität (das Cogito) die Welt der Extensität beleuchtet. In diesem Gedanken treffen sich Descartes' Individualismus und Urform-Sensibilität.
Der Ursprungspunkt (Origo) repräsentiert jenes aktive Verhalten, das Lajos Szabó "teilende Attitüde" nennt: Es hebt den "an sich"-Charakter der Ebene, der ebenene Richtungen auf, bezieht sie auf sich und zerlegt sie mittels einer aus dem Zentrum (aus sich selbst) strahlenden vertikal-horizontalen Gliederung.
Descartes' Origo-Struktur repräsentiert den Logos, der seine Identität mit dem Zentrum dadurch zum Ausdruck bringt, daß er den Richtungsraum, mit dem er konfrontiert wird, durch Gliederung zerlegt, wertet, auf sich, das Origo bezieht.
8. Durch das Origo dringt die ganze Welt der Individualität in die Geometrie ein (die affine und die projektive Geometrie nehmen Gestalt an). Im tiefsten Innern jeder Individualität lebt das gleiche ungebrochene Ganze, dads gleiche ungeteilte eine, teilende und messende Subjekt, das Béla Tábor als Persönlichkeit bezeichnet und das vom Origo, vom Ursprungspunkt zum Ausdruck gebracht wird. Doch in der Individualität steckt auch die Welt der Geteiltheit, der Gebrochenheit. Diesen Widerspruchsherd der Individualität stellt die hyperbolische Geometrie in den Mittelpunkt: Mit Nachdruck vergegenwärtigt sie das Bestreben aller Punkte, Origo zu sein. Durch die Analyse dieses Widerspruchsherdes sprengt sie die Stabilität des wissenschaftlichen Paradigmas (das euklidische Paradigma ist das Paradigma der Paradigmen), um zu einer dynamischeren geometrischen Rechtwinkel-Struktur zu gelangen.
9. Zum einen demonstrieren Bolyai/Gauss/Lobatschewskij den Widerstand, der die Tranparenz der geometrischen Rechtwinkel-Struktur bricht, zum anderen möchten sie diese Rechtwinkel-Struktur erneuern. Erneuern kann man sie aber nur aus ihrem Mittelpunkt, dem Origo, und nur in dem Maße wie es gelingt, das erschlossene Widerspruchssystem der Individualität in das Innenleben des Origo zurückzuleiten und durch seine tiefere Darlegung aufazuheben (vgl. Subjektivierung der Widerstände).
Auf das Sichtbarwerden der Brechungspunkte der Individualität wurde bereits bei der Analyse der Brechung der parallelen Halbgeraden verwiesen. Doch wenn man diese Brechung nicht von seiten der Geraden, sondern des Punktes betrachtet, erlischt das störende Gefühl der Diskontinuität unverzüglich, und an seine Stelle tritt die große raumschaffende Kraft des Punktes. Die ganze Gerade paßt in einen, in einem Punkt ansetzenden Winkelraum (Abb. 2). Die beiden Enden der Geraden divergieren nicht so wie bei Euklid. Im Raum einer Subjektivität läßt sich all das impliezieren und durch ihre Präsenz intensivieren, eas die Gerade über den Angangs- und Endpunkt aussagen kann. Im Raum des Punktes kommt all das zusammen, was sich früher an den "zwei Enden" der Gerade im Nebel des entthronten Mythos verlor.
Als Ausgangspunkt holt sich der Punkt große Territorien seiner bei Euklid verlorenen Intensität und raumschaffenden Fähigkeit (seines Innenraums) wieder. Andererseits wächst der Bedeutungsinhalt des Unendlich-Fernen spürbar; sein Eros ist größer als bei Euklid. (Vor unseren Augen erscheint zwar nicht das Unendlich-Ferne, aber die Beziehung zwischen den beiden Momenten: Zwei beliebige unendlich-ferne, "ideale" Punkte sind stets durch eine wirkliche Gerade verbunden.) Bei Bolyai/Gauss/Lobatschewskij strebt der Abstand der Parallelen nach Null, zeigen also viel deutlicher auf einen gemeinsamen Punkt. Doch trotz aller Annäherung bestehen auch Gegensätze zwischen ihnen, deren Aufhebung sie dem nicht mehr sichtbaren Unendlichen außerhalb der Ebene überlassen.
10. Bolyai/Gauss/Lobatschewskij wollen die Bedeutung des unendlich-fernen Punkt näher bringen, damit das Ideale, das Unendlich-Ferne hier und jetzt Gewicht habe, sich von der deistischen ideologischen Rahmenfunktion abhebe und in der manifesten Welt der Gegensätze wirken könne; damit das überzeitliche Zentrum jenseits von Geburt und Tod auch für das zwischen Geburt und Tod gezwängte Individuum ein Gewicht habe, das sich auf sein ganzes Sein auswirke. Ihre Bemühungen treten – das ist ihr innerer Widerspruch – in zwei, nicht vereinheitlichten (divergierenden) Richtungen zutage: Zum einen behalten sie das Unendlich-Ferne bei, verleihen nur dem Hinweis mehr Gewicht, zum anderen wollen sie das Widerspruchsystem der Individualität hier und jetzt der Rechtwinkel-Struktur des Origo gegenüberstellen.
11. Ihr starkes – allerdings noch mit Widersprüchen belastetes – Bestreben, das Unendlich-Ferne näherzubringen, erschließt hinter der euklidischen Fläche Flächen mit bislang unbekannter Geometrie. Diese Formen, die eine höhere dramatische Spannung haben, können wir nur dann sehen und verstehen, wenn wir uns die dynamischere Anschauungsweise von Bolyai/Gauss/Lobatschewskij und ihre Bemühungen, die diese Formen erzeugten, zueigen machen.
Geniale Mathematiker können der Mathematik eine neue Richtung geben, weil sie daran glauben, daß die Wahrheit tiefer liegende, noch unmathematisierte Bereiche hat, die sie dann in mathematische Formen fassen. Das produktive Verständnis diesen Formen bedeutet nicht nur formales Verständnis, sondern auch die wertende Aneignung des Glaubens und der Weltauffassung, die die Formen zustande bringen und beleben. Aber sie bedeuten auch ihre radikale Weiterführung: Wir können nicht verharren beim Näher-bringen des unendlich-fernen Punktes und den damit verbundenen Widersprüchen – wir müssen ihn ins Zentrum unseres Seins, unserer Gegenwart zurückholen. Was Bolyai/Gauss/Lobatschewskij in einer Sprache, die ans Paradigma der das Zentrum in die Unendlichkeit schiebenden Parallelen gebunden war, und demzufolge in zwei, noch divergierenden Richtungen formulierten, das müssen wir auf ihr gemeinsames Zentrum beziehen: umdefinieren im Raum der pythagoreischen Auffassung, die dadurch erneuert wird, daß das Zentrum wirklich in den Mittelpunkt gestellt wird.
12. Wir identifizieren uns insofern mit jeder Erkennungsform als sie den überzeitlichen Anfangs- und Endpunkt unseres Daseins sowie die Widersprüche, die die stete zeitliche Präsenz des überzeitlichen Zentrums verursacht, mit ihrer ganzen Energie ergreift und auf diesen tiefsten aktuellen Widerspruch unsere aktuellen Widersprüche zurückführt. Wo sich uns Gelegenheit zu dieser Identifikation bietet, dort lieben wir. Unabänderlich. Und wo Bolyai/Gauss/Lobatschewskij bei ihren aktuellen Widersprüchen stehenbleiben und sie nicht auf den Urwiderspruch des konkreten Daseins des Logos zurückführen, selbst dort müssen wir uns darum bemühen, diese Widersprüche vom Urwiderspruch des Logos aus zu deuten und aufzuheben.
Übersetzung: Madelein MERÁN
![]()
![]()
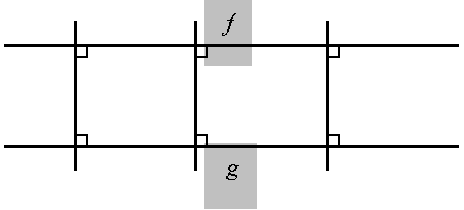
Abbildung 1. (In
der euklidischen Geometrie gültig) f
und g sind Parallelen, ihr Abstand
ist konstant; durch alle Punkte der Ebene geht eine, zu f und g senkrechte
Gerade; es gibt ein Quadrat; die Transparenz der Rechtwinkel-Struktur. Tragik:
der gemeinsame (Begegnungs-)Punkt ist ins Unendliche verschoben.
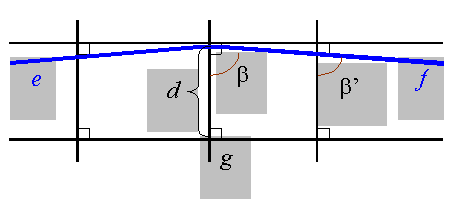
Abbildung
2. (In der
hyperbolischen Geometrie gültig) e
ist parallel zu g nach links, f ist parallel zu g nach rechts; Brechung:
der Winkel von e und f ist kleiner als 180°; die
raumschaffende Kraft des Punktes: der
durch e und f begrenzte Winkelraum enthält g
vollständig (b wird beliebig klein, wenn d groß genug ist).
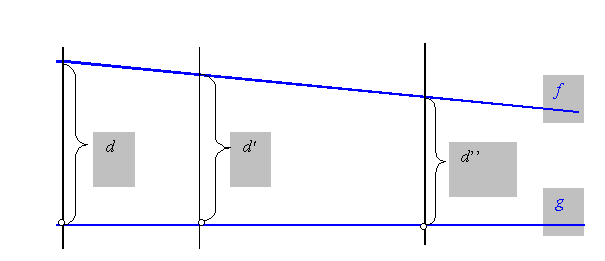
Abbildung
3. (In der
hyperbolischen Geometrie gültig) f
und g sind Parallelen (nach rechts),
sie haben keine gemeinsame senkrechte Gerade; sie sind asymptotische Geraden, ihr Abstand strebt nach Null: d wird beliebig klein, wenn P auf der Gerade (nach rechts) ins
Unendliche gleitet.
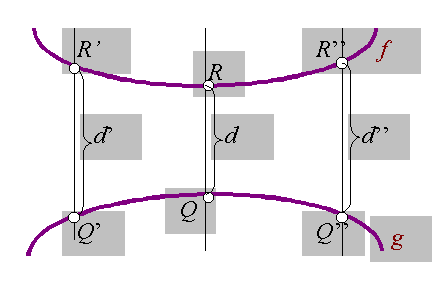
Abbildung
4. (In der
hyperbolischen Geometrie gültig) f
und g sind ultraparallele Geraden. Sie haben genau eine gemeinsame
senkrechte Gerade; es gibt kein Quadrat; d
wird beliebig groß, wenn R und Q auf der Gerade ins Unendliche gleiten.