SURÁNYI LÁSZLÓ:
Descartes, Bolyai és
Lobacsevszkij:
A geometria visszavezetése szubjektív gyökerére[1]
1. Míg a centrum köré vont kör zártságával az esztétikai mozdulatot, a magába fogadás mozdulatát jeleníti meg, addig az egyenes az aktív etikai mozdulatot, a „te” felé fordulást, a távolság-teremtést és a távolság legyőzését, a Szabó Lajos-i „előre és felfelé törő rangrelativitást”, a centrum mozgását. Kép és tűz, főnév és ige, böhmei Wesen és Geist, formálás és teremtés.
De az euklideszi sík egyenese, pontosabban a párhuzamos egyenespár egy ezzel ellentétes, tehetetlenséget kifejező mozdulatot is megjelenít, sőt végtelenít: azt a mozdulatot, amellyel a centrumot, mely egyszerre kezdő- és végpont, kiengedjük szemléletünk teréből, jelentése elhalványul, és többé nem tudunk vele azonosulni.
2. Az irány mutatás, az azonos irány közös pontba, közös középpontba mutatás. A közös centrum nem puszta matematikai pont, belső tere van (mint ahogy ez modern, funkcionalizált változatáról, a nullvektorról is leolvasható): minden iránnyal van benne azonos, és minden irányra van benne merőleges (ami a dimenzió-növekedés geometriai jele). Az origó minden azonosításnak (az ellenállások önmagára vonatkoztatásának) és minden transzcendálásnak, minden dimenziónövekedésnek a forrása. A két irány: szubjektivizálás és transzcendálás, önmagamra vonatkoztatás és énem határainak tágítása nincs egymás nélkül, csak mint a derékszög két szárának két egymást erősítő iránya.
Ezt a végső közös identifikációs pontot, az egy irányba tartók egymásra-vonatkoztatásának, találkozásának pontját tolja a végtelenbe az euklideszi párhuzamosok képe (a metsző egyenesek esetében pedig belső tér nélküli puszta matematikai pontra redukálja).
Az euklideszi párhuzamosok távolsága itt állandó. A párhuzamos egyenesek egy olyan közösség képét nyújtják, amelynek tagjai már kiléptek a közös mítoszból, de nem lépnek be a logosz terébe; önmaguk felé fordulnak, és megmaradnak egymástól egyforma távolságban pályájukon, közeledés és távolodás, találkozás és búcsú nélkül.
A párhuzamosoknak sem a múltjukban, sem a jövőjükben, sem a jelenükben nincs közös pontjuk. A közös múltból a régmúltba, a kiürült, trónfosztott mítoszba süllyedt, a jővőből pedig az elérhetetlen távolba illant. A párhuzamosokban egy olyan közösség képét látjuk, amelynek tagjai együtt, de egymástól áthidalhatalan távolsággal elválasztva szemlélik azt, ami a régmúlt, és az elérhetetlen távol ködös mítoszaiba vonult vissza. A közösen szemléltet sem közös genezisként, sem közös megváltásként nem tudják megjeleníteni.
Az euklideszi sík az ananké, a megszólíthatatlan szükségszerűség síkja.
3. Ezen a centrumát vesztett síkon azonban létezik a síkformák hasonlósága. A görög pozitívum: eleven formákat teremteni a tragikus háttéren. Az örök nem-találkozás hátterén eleven formák összehasonlíthatósága. Az absztrakt-archaikus geometriai alakzatok dinamikus összevetése: kicsinyítése és nagyítása.
A mérés mértékegysége a pythagoreus alapalakzat, az egységnégyzet. A párhuzamossági axióma pozitív tartalma: az egységnégyzet azonsosága az egész síkon transzparensen jelen van. Kicsinyíthetősége és nagyíthatósága minden mérés alapja.
4. A síkformák kicsinyíthetősége-nagyíthatósága és megváltoztathatatlan ananké, látható pythagoreus alapformák és láthatatlan törés – Bolyaiék (ún. hiperbolikus) geometriája mindezt visszájára fordítja. A modern tragikumot manifesztálja a matematika nyelvén.
a) Bolyaiék bevezetik a geometriába az aszimptotikus egyeneseket. Az ő párhuzamosaik aszimptotikus egyenesek. Rendeltetésük az lenne, hogy találkozzanak (távolságuk nullához tart). És mégsem találkoznak (3. ábra).
Ezzel szemben: az origó-gondolat értelme az, hogy a látszatra legjobban széttartó egyenesek is találkoznak; egymáson értelmeződnek. A találkozás a kölcsönös belső érdekeltség terében történik. Iránytalan, közömbös egyenesek, gondolatmenetek, amelyeknek nincs céljuk és súlyuk, azaz nincs legyőzött belső ellenállásuk, nem találkozhatnak. A centrum, az origó belső tere a találkozás helye.
b) Bolyaiék egyenesei súlyosabbak, mert nagyobb ellenállást sűrítenek magukba és győznek le, mint Euklidészéi. De még ellenállás és centrum dualizmusában élnek.
Bolyaiék a külső pontból ugyanahhoz az egyeneshez két irányban húzott párhuzamos félegyenes között törést állapítanak meg (2. ábra). Ezzel a maguk módján láthatóvá teszik az egyenesben rejlő ellentétes, széttartó erőket. Az euklideszi egyenesnek csak egy „ideális”, „végtelen távoli” pontja van, az ő egyenesüknek kettő, náluk tehát már nem mosódik úgy össze kezdő- és végpont, mint Euklidésznél, mindkettőnek megkülönböztethető belső mondanivalója van a jelenben. De az egyenes szemszögéből nézve a kettő között nincs kontinuitás, hanem törés van, minden pont törésponttá válik.
Bolyaiék párhuzamos egyenespárja a modern tragikum képe: láthatóvá teszi az euklidesziben még láthatatlan törést. A jel és jelzett közötti láthatatlan törés a jelben is láthatóvá válik.
5. Az euklideszi sík tehát „megfordul”, visszajáról látszik Bolyaiéknál. Előtérbe kerül a a feszülő tragikum, az ellentétek világa, a széttartás (a Bolyai-tér közeli rokonságban áll Vajda Lajos örvénytereivel[2]), háttérbe szorul viszont az összehasonlíthatóság, a böhmei Leiblichkeit, a rosenzweigi Lebendigkeit formagazdag világa: a hiperbolikus síkon nincs hasonlóság, kicsinyíthetőség és nagyíthatóság. Nehezebben érhető el, hogy két egyenes messe egymást. Nehezebben születnek háromszögek, határolt síkformák, mert a tragikum, a közelítő párhuzamosok, a találkozásra-rendeltek találkozását gátlő örvények a síknak sokkal nagyobb és hangsúlyosabb részét foglalják el. Nagyobb ellenállást kell legyőzni a forma (egyenes, háromszög) születéséhez, a születő forma viszont súlyosabb. Individuálisabb is: nagyobb az ellenállása a méréssel, az összehasonlíthatósággal szemben. A mérés a „görbültség” miatt nehezebbé válik (de véglegesebb: létezik abszolút távolságegység, és létezik maximális, minden háromszöget magában foglaló háromszög). A derékszög-struktúra transzparenciája megtörik: nincs négyzet.
(Kézenfekvő a Bartók-párhuzam. Rá is jellemző a klasszikus alakzatok mögött meghúzódó törések szigorú, a zeneileg széppel látszólag szembefeszülő megmutatása.)
6. Bolyaiék úgy látják, hogy a nagyobb (és végső soron maximális) értékre törekvés vertikálisa és a minimális értékek biztosításának horizontálisa, e két alapirány közti kiegyensúlyozott viszony, amely egy megismerő korszak stabilitását és produktivitását (és történelmi korokon átívelő egységét) biztosította, elvesztette transzparenciáját. A derékszög-szimbólum mélyebb jelentéséhez – az origóból sugárzó derékszög-struktúra mélyebb feltárásához – akarnak eljutni, s ehhez csak úgy juthatnak el, ha a transzparenciával szmebeni ellenállásoknak (és a derékszöggel szembeni ellenállásoknak is) a gyökeréig ásnak le, s azt állítják középpontba. Ez az ellentmondásgóc: az egyéniség. Bolyaiék forradalma az egyéniésg forradalma.
7. Ezt a forradalmat Descartes gnosztikus origó-gondolata indította el, amelynek alapján Descartes aritmetizálja az euklideszi geometriát, hogy megalapozza azt. De origó-gondolata szembeszáll a centrumnak és az ellenállásoknak az euklideszi párhuzamosoknál látható végtelenbe vetítettségével, valamint a pont belső terének a síkban való szétszórtságával. Míg az euklideszi szemlélet (a hiperbolikus is) a belső tér nélküli, matematikai pontból és egyenesből indul ki, mint alapfogalomból (az intenzitás felé mutató irány fogalmát alárendeli az extenzív egyenes fogalmának), addig Descartes középpontba állítja az origót, a centrumot, és a belőle sugárzó alapirányokat: a vertikális és a horizontális tengelyt. Az origó a kezdőpont, ahol a cogito biztos kiindulópontként tör be a sum világába, és világítja meg a sum struktúráját: vagyis azt, hogy ez a sum maga az időfölötti vertikálisának és az időbeliség horizontálisának metszéspontjában áll.
A mítosz alapirányainak, fentnek és lentnek, elölnek és hátulnak abszolút jelentését megingató, illetve relativizáló kopernikuszi fordulattal ellentétes fordulatként a descartes-i matematikában megjelenik a kitüntetett pont, a kitüntetett irány és harmadikként a kitüntetett síkalakzat, a kúpszeletek (kör, ellipszis, parabola stb.) közös ősképe: az egységkör. Descartes egyik legszebb gondolata ez az origó-szerkezet, amellyel az intenzitás (a cogito) megvilágítja az extenzitás világát. Descartes individualizmusa és ősforma-érzékenysége találkozik e gondolatban.
Az origó azt az aktív magatartást képviseli, amelyet Szabó Lajos osztó magatartásnak nevez: megszünteti a sík, a síkbeli irányok „an sich” jellegét, magára vonatkoztatja és felbontja őket a centrumból (önmagából) sugárzó vertikális-horizontális tagolással.
A descartes-i origó-szerkezet a logoszt képviseli, amely a centrummal való azonosságát úgy fejezi ki, hogy a centrumból sugárzó vertikális-horizontális tagolással felbontja, értékeli, önmagára, az origóra vonatkoztatja azt az irányteret, amellyel szembesül.
8. Az origón keresztül az egyéniség egész világa betör a geometriába (alakot ölt a projektív és az affin geometria). Minden egyéniség legmélyén ugyanaz a töretlen egész, ugynaz az osztatlanul egy, osztó és mérő alany él, ezt nevezi Tábor Béla személyiségnek. Ezt fejezi ki az origó. De az egyéniségben benne van az osztottság, a törtség világa is. Az egyéniségnek ezt az ellentmondásgócát állítja középpontba a hiperbolikus geometria: nyomatékkal megjeleníti minden pontnak azt a törekvését, hogy origó legyen. Ennek az ellentmondásgócnak az elemzésével felrobbantja a tudományos paradigma stabilitását (az euklideszi paradigma a tudományos paradigmák paradigmája), hogy egy dinamikusabb derékszög-struktúrához jusson el.
9. Bolyaiék egyrészt megjelenítik a geoemtriai derékszög-struktúra transzparenciáját megtörő ellenállást, másrésztr meg akarják újítani ezt a derékszög-struktúrát. De megújítani csak középpontjából, az origóból, az origó belső teréből lehet, és csak annyiban, amennyiben sikerül az origó belső életébe visszavezetni és annak mélyebb kifejtésével feloldani az egyéniség feltárt ellentmondásrendszerét (vö. az ellenállások szubjektiválása).
Az egyéniség töréspontjainak láthatóvá válására már rámutattunk a párhuzamos félegyenesek törésének elemzésénél. De ha ezt a törést most nem az egyenes, hanem a pont oldaláról nézzük, a diszkontinuitás bántó érzése rögtön megszűnik, és helyére a pont nagyerejű térszerűsége lép. A teljes egyenes belefoglalható egy egy pontból induló szögtartományba (2. ábra). Az egyenes két vége nem tart úgy szét, mint Euklidésznél. Egy szubjektivitás terébe foglalható és a jelenlét intenzitásával felizzítható mindaz, ami mondanivalója lehet az egyenesnek a kezdő- és végpontról. A pont terébe összefuthat mindaz, ami korábban az egyenes „két végén” a trónfosztott mítosz ködébe tűnt.
A pont mint kiindulópont nagy területeket hódít vissza az Euklidésznél elveszett intenzitásából és térteremtő képességéből (belső teréből). Másrészt érezhetően megnő a végtelen távoli jelentéstartalma; nagyobb az erosza, mint Euklidésznél volt. (Ha maga a végtelen távoli nem is, de a két mozzanata közti kapcsolat megjelenik szemünk előtt: bármely két „végtelen távoli, ideális” pontot egy valódi egyenes köt össze.) Bolyaiék párhuzamos egyenesei „minden határon túl közelednek egymáshoz”, s így sokkal inkább mutatnak egy közös pont felé. De minden közeledés ellenére ellentét is feszül köztük, ennek feloldását a beláthatatlanba, a síkon túlra kitolt végtelenre bízzák.
10. Bolyaiék arra törekednek, hogy közelebb hozzák a végtelen távoli pont jelentését, hogy az „ideálisnak”, a végtelen távolinak itt és most súlya legyen, kiemelődjék deista ideologikus keretfunkciójából, és hatni tudjon az ellentétek manifeszt világában; hogy a születés és halál közé zárt individuum számára is egész létére kiható súlya legyen a születésen és halálon túli, időfölötti centrumnak. Törekvésük – ez belső ellentmondásuk – két, nem egységesített (széttartó irányban) jelentkezik: egyrészt megtartják a végtelen távolit, csak nagyobb súlyt adnak a rá mutatásnak, másrészt az egyéniség ellentmondásrendszerét akarják itt és most szembesíteni az origó derékszög-struktúrájával. Itt és most: mert az origó és a belőle sugárzó derékszög-struktúra az egyéniség saját belső mértéke.
11. Erős Erős – bár még ellentmondásokkal terhes – törekvésük, hogy közelebb hozzák a végtelen távolit, új, eddig ismeretlen geometriájú felületeket tár fel az euklideszi felület mögött. Ezeket a nagyobb drámai feszültséget hordozó formákat csak akkor látjuk és értjük meg, ha elsajátítjuk Bolyaiék dinamikusabb szemléletmódját, és magunkévá tesszük törekvésüket, amely e formákat létrehozta.
A zseniális matematikusok azért tudnak új irányt kijelölni a matematikának, mert hisznek abban, hogy az igazságnak vannak belsőbb, még matematizálatlan körei, és ezeket a bel¬sőbb köröket foglalják matematikai formába. E formák produktív megértése nemcsak formális megértést, hanem a formát létrehozó és éltető hit és világfelfogás értékelő elsajátítását jelenti. De radikális továbbvitelét is: nem állhatunk meg a végtelen-távoli pont ilyen közelebb-hozásánál s a vele járó ellentmondásoknál, létünk, jelenünk centrumába kell visszahelyeznünk. Amit Bolyaiék a centrumot a végtelenbe kitoló párhuzamosok paradigmájához kötött nyelven, s ezért két, még széttartó irányban fogalmaztak meg, azt nekünk közös centrumukra kell vonatkoztatnunk: egy megújított – a centrum valódi, minden értelemben való középpontba helyezése révén megújított – pythagoreus szemlélet terében kell újraértelmeznünk.
12. Minden megismerési formával annyiban azonosítjuk magunkat, amennyiben teljes energiájával megragadja létünk időfölötti kezdő- és végpontját s az ellentmondásokat, amelyeket az időfölötti centrum folytonos időbeli jelenléte okoz: aktuális ellentmondásainkat erre a legmélyebb aktuális ellentmondásra vezeti vissza. Ahol erre az azonosításra alkalmunk nyílik, ott szeretünk. Visszavonhatatlanul. Ahol pedig Bolyaiék megállnak az aktuális ellent-mondásaiknál, nem vezetik vissza a logosz konkrét létezésének erre az ősellentmondására, nekünk ott is arra kell törekednünk, hogy innen értelmezzük és oldjuk fel ellentmondásaikat. [3]
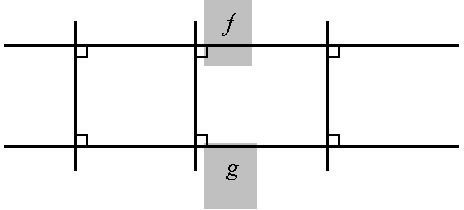
1. ábra (az euklideszi geometriában érvényes): f és g (mindkét irányban) párhuzamosak, távolságuk állandó, a sík minden pontjából húzható hozzájuk közös merőleges; van négyzet, a derékszögstruktúra transzparenciája. Tragikum: a közös pont (metszéspont: találkozási pont) a végtelen távolba van kitolva.
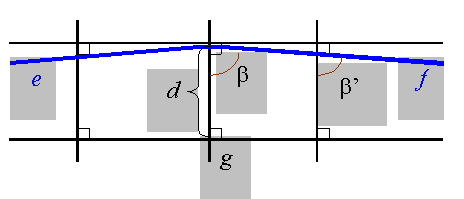
2. ábra (a hiperbolikus geometriában érvényes): e balra, f jobbra párhuzamos g-vel; töréspont: e és f szöge kisebb 180°-nál; a pont térteremtő ereje: e és f által alkotott szögtartomány teljesen magában foglalja a g egyenest, ez a szög tetszőlegesen kicsi lehet: b tetszőlegesen kicsi, ha d megfelelően nagy.
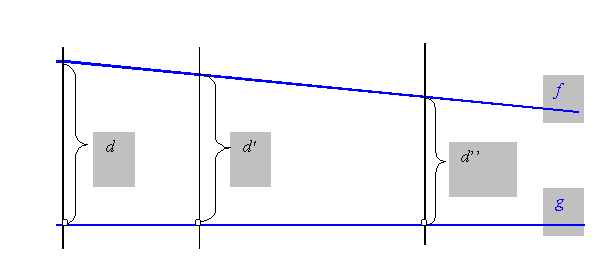
3. ábra (a hiperbolikus geometriában érvényes): f és g (jobbra) párhuzamos egyenesek, nincs közös merőlegesük; aszimptotikus egyenesek: a távolságuk nullához tart, ha P a g egyenesen tart a végtelenbe.
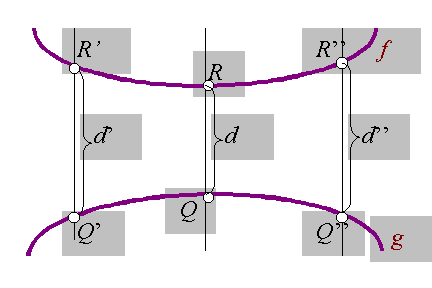
4. ábra (a hiperbolikus geometriában érvényes): f és g ultraparallel egyenesek. Pontosan egy közös merőlegesük van, ahol legkisebb közöttük a távolság, mindkét irányban végtelenhez tart a távolságuk, ha R és Q tart a végtelenbe.